호랑이조림

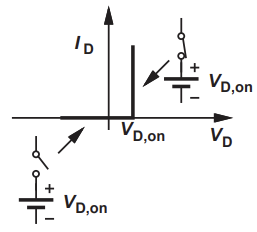
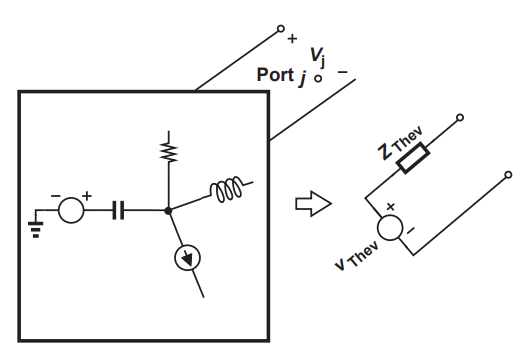
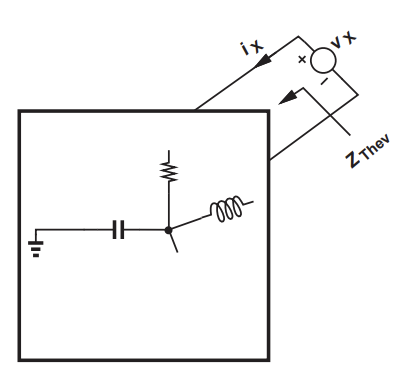
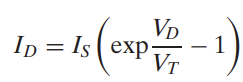BJT나 mosfet으로 amplifier를 설계할 때, 갖춰져야 하는 조건들이 있다.

특정한 동작 영역에 존재하게끔 한다거나, PVT variation에 덜 민감해야한다던가...

이런 조건들을 갖춰줌으로써 회로가 원하는대로 동작하게끔 환경을 조성해주는 것을 Biasing이라고 한다.

Simple Biasing으로부터 시작하여 간단한 Biasing 기법들에 대해 알아보자.

위와 같은 구조가 Simple Biasing 이다. Base-Emitter 에 순방향 전압을 걸어줄 수 있으며, 저항 값을 적절히 조절하여 Collector-Base에 역방향 전압을 걸어줄 수 있다.

보통 BJT 규격상 V_BE가 700mV ~ 800mV가 되게끔 설계하며 이에 맞게 R_B와 R_C를 설정해주면 된다.

다만 단점이 많은 회로인데,

1. V_BE가 조금만 달라져도 I_C가 크게 바뀌어, 회로의 동작 영역이 불안정해진다.

2. 트랜지스터의 β 의 변화에도 매우 민감해진다. 예를 들어 β가 조금만 증가해도, I_C가 증가함에 따라서 V_CE가 감소하고, 결구 V_CB가 감소함에 따라서 트랜지스터가 saturation 영역에 가까워지게 된다. 즉, 이 역시 회로의 동작 영역이 불안정해지게 되는 것이다.

여기서 β dependency를 해결한 것이 Voltage-divide biasing이고, V_BE dependency를 해결한 것이 Emitter-Degeneration 이다.

R_2를 추가한 것이 Voltage-divide, R_E를 추가한 것이 Emitter-Degeneration 이다.

먼저 Voltage-divide의 이점을 보자.

Simple-Biasing에서는 V_X가 비교적 일정한 값으로 유지되지 않았고 변동성이 컸다.

때문에 V_BE가 변동되고 I_C가 변동되고 β 값에 따라 I_B도 변동되고 또 V_BE가 변동되고...

이 과정대로라면, β 값에 따라 동작 영역이 불안정해질 수 있다.

하지만 Voltage divide로 V_X를 비교적 안정된 상태로 유지시켜주면, BJT의 전류 공식에 따라서 I_C 또한 비교적 안정된 상태가 된다.

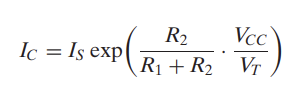
물론 이를 만족시키기 위해서는, 베이스 전류가 충분히 작아 V_CC에서 GND로 흐르는 대전류가 베이스로 거의 빠져나가지 않아 V_X가 일정하게 유지된다는 조건이 필요하다. 이를 위해 R1과 R2의 값을 적절하게 선택하는 것이 중요하다.

Emitter-Degeneration은 V_BE dependency를 줄여준다.

만약 R_E가 없다면 어떨까?

V_BE와 I_C는 지수함수 관계이기 때문에 V_BE의 조그마한 변화에도 I_C가 크게 변하게 된다.

하지만 R_E를 추가해준다면?

V_BE가 오르면 I_C가 오르고 I_E가 증가함에 따라 V_E가 증가해서, V_BE가 작아지는 negative-feedback 이 이루어진다. 따라서 V_BE를 비교적 일정하게 유지시켜주게 된다.

물론 이렇게 V_BE의 변동성을 줄여주기 위해 V_RE가 충분히 커야한다는 조건이 있다.

이름이 Emitter-Degeneration인 이유는 이미터단에 저항을 추가함에 따라 Gain이 작아지는 소소한 단점이 있기 때문인데, Biasing에 있어서 아주 큰 이점을 갖기 때문에 유용한 Biasing 기법이다.

참고로 이 회로에서 R_C가 충분히 작아야 V_C가 커져, BJT가 active mode에 존재할 수 있다는 조건이 있다.

마지막으로, Self-Biasing이라는 Biasing도 있다.

R_B에서 이루어지는 전압강하를 통해 V_YX > 0을 항상 만족시켜줌으로써 트랜지스터가 항상 active mode에 있게 해주는 기법이다. R_C가 아무리 커지더라도 회로가 무조건 active mode에 있을 수 있다는 장점이 있다.

또한, speed 면에서 이점이 있다고도 한다.

mosfet 또한 위와 같이 Biasing 하면 된다. 다만, mosfet은 gate 전류가 0이기 때문에 훨씬 편하게 biasing할 수 있다. 이는 mosfet이 BJT에 비해 갖는 큰 장점이기도 하다.

이러한 Biasing 기법들 외에도, 다양한 기법들이 있다고 한다. current mirror를 사용한다던가... 기타 등등.

전공교재를 벗어난 많은 기법들이 연구되어 있다고도 한다.

어쨌든 핵심은 일정한 전류나 전압을 유지시켜 소자를 원하는 동작 상태에 있게 하는 것이다.

일반적으로 회로는 다이오드, 트랜지스터, 기타 등등... 다양한 active 소자로 이루어진다.

그런데 이러한 소자들은 전류와 전압의 관계가 이차함수, 지수함수, 로그함수 등의 복잡한 관계를 가진다.

이를 선형적인 관계로 근사시킬 수 있는 것이 바로 Small signal(소신호) 기법이다.

예시를 하나 들어보자.

위와 같은 회로에서 V_ad를 3V에서 3.1V로 올렸을 때, V_out은 어떻게 변할까?

다이오드에 걸리는 전압과 R1에 걸리는 전압을 합친 값이 3.1V가 돼야한다.

저항의 전류와 전압의 관계는 linear인데, 다이오드는 관계가 exponential이다.

구해보면 알겠지만... 바로 구할 수 있는 마땅한 방법이 없어서 iteration을 통해서 구해야 하는데, 이 과정이 시간이 오래 걸린다. iteration을 하면 약 2.411V라는 값이 나온다.

여기서 small signal을 활용할 수 있다.

위 그림에서 A점에서 B점으로 값이 변한다고 하자. 전에 말했던 예시에서도 볼 수있듯이 exponential한 관계를 그대로 적용하여 B로의 변화된 값을 측정하려 하면 상당히 복잡해진다.

하지만 A에서 B까지의 변화가 linear하다고 근사시키면...?

즉 A에서의 접선을 통해 B값을 구한다면 굉장히 편해질 것이다. 물론, V_D의 변화가 충분히 작아야 오차가 적어질 것이다.

다이오드의 관계식에서 미분을 통해 접선의 기울기를 이렇게 구할 수 있다. 

전류나 전압의 변화를 이렇게 linear한 관계로 표현할 수 있게 된다.

그런데 이렇게 작은 변화를 linear한 관계로 표현할 때, 변화 지점이 어디인지에 따라서 기울기가 달라질 수 있다.

변화되는 지점, 위에서는 A 지점을 "bias point", "operation point"라고 하며 A 지점의 신호를 Large-signal이라고 한다.

보통 회로에서 Large-signal을 먼저 분석한 후, 이 지점에서의 기울기를 구해 Small-signal로 간단하게 분석할 수 있다.

트랜지스터를 사용한 amplifier 등에서도 이는 유용하게 사용된다.

트랜지스터를 적절하게 biasing 해주면 transconductance를 구할 수 있고, small signal과 transconductance를 활용하여 Small signal의 변화에 따른 시스템의 출력의 변화를 쉽게 구할 수 있다.

다이오드는 p형 반도체와 n형 반도체를 접합시켜 만든 소자다. 위와 같은 기호로 나타낸다.

Vanode - Vcathode = V_D 라고 할 때,

V_D > 0 이면 forward-biased 되어 전류가 흐르고

V_D < 0 이면 reverse-biased 되어 전류가 흐르지 않는 것이 이상적인 다이오드의 동작이다.

즉, 순방향 전압일 때  닫힌 스위치, 역방향 전압일 때 열린 스위치의 역할을 해준다고 보면 된다.

이상적인 다이오드의 I-V characteristics 이다. reverse bias일 때는 저항이 무한대인 것처럼, forward bias일 때는 저항이 0인 것처럼 동작한다.

그러나 이는 이상적인 다이오드의 동작이다. 실제 다이오드는 I와 V가 지수함수꼴의 관계를 갖는다.

전류와 전압의 관계가 지수함수꼴이면 나중에 회로가 복잡해질 때 값을 구하기가 복잡해질 수 있다. 이 때

이렇게 constant-voltage model로 더 쉽게 다이오드의 동작을 설명할 수 있다.

회로를 분석할 때 유용한 스킬들이 있다. 회로가 복잡해지면 특히 필요한 스킬들이다.

1. Kirchoff Current Law

회로의 어떤 한 노드로 흘러 들어가는 전류의 합은 무조건 0이다.

위 그림에서 I1, I2, ... In 을 전부 합하면 0이 나와야한다.

2. Kirchoff Voltage Law

회로의 어떤 한 폐회로의 voltage drop의 합은 무조건 0이다.

위 그림에서 V1 + V2+ V3 + V4 = 0 이다.

위에서는 2가지 법칙을 쉬운 그림으로 설명했지만, 회로가 복잡해질수록 특정 component의 전류나 전압을 측정하기가 까다로워질 수 있다. 이때 키르히호프 법칙을 이용하면 여러 linear equation들을 만들 수 있고, 이를 연립하여 전류나 전압을 구할 수 있다.

3. Thevenin Equivalent

두 노드 사이에 복잡한 회로가 존재할 때, 이를 전압원과 임피던스를 갖는 소자가 직렬로 연결돼있는 간단한 회로로 치환할 수 있다.

이 때 테브닌 등가전압 V_thev는 회로의 port(두 node)를 open 시킨 후, 전압을 측정하면 구할 수 있다.

위 그림에서 V_j가 V_thev라고 볼 수 있다.

등가 임피던스 Z_thev는 회로의 port에 임의의 voltage source 를 인가했을 때, voltage source의 전압과 전류비로 구할 수 있다. 이때, 독립전압원은 short시키고, 독립전류원은 open 시켜야한다.

위 그림에서 V_x/i_x = Z_thev 이다.

4. Norton equivalent

두 노드 사이에 복잡한 회로가 존재할 때, 이를 전류원과 임피던스를 갖는 소자가 병렬로 연결돼있는 간단한 회로로 치환할 수 있다.

노튼 등가전류 i_nor 는 회로의 port를 short 시키고 전류를 측정하면 구할 수 있다.

노튼 등가 임피던스는 테브닌 임피던스와 똑같이 구하면 된다.

즉, Z_thv = Z_nor 이다.

테브닌 등가회로나 노튼 등가회는 특정 port에 존재하는 load가 달라질 때 유용하게 사용할 수 있다.

등가회로를 사용하지 않으면 load의 전압이나 전류를 다시 복잡한 과정을 거쳐 구해야하지만, 등가회로를 사용하면 훨씬 쉽게 구할 수 있다.